SIMPANGAN RATA-RATA, RAGAM
DAN STANDAR DEVIASI
SIMPANGAN RATA-RATA
Rumus Simpangan Rata-Rata
Contoh 1:
Diberikan data sebagai berikut:
5, 6, 8, 5, 7Tentukan nilai S data di atas!
Langkah awal terlebih dulu temukan rata-rata datanya:Setelah diketahui rata-ratanya, saatnya mencari S:
RAGAM (VARIAN) DAN SIMPANGAN BAKU (STANDAR DEVIASI)
Varian dan standar deviasi (simpangan baku) adalah ukuran-ukuran keragaman (variasi) data statistik yang paling sering digunakan. Standar deviasi (simpangan baku) merupakan akar kuadrat dari varian.
Oleh karena itu, jika salah satu nilai dari kedua ukuran tersebut diketahui maka akan diketahui juga nilai ukuran yang lain.Penghitungan
Namun cara seperti itu tidak bisa digunakan karena hasilnya akan selalu menjadi 0.

Oleh karena itu, solusi agar nilainya tidak menjadi 0 adalah dengan mengkuadratkan setiap pengurangan nilai data dan rata-rata kelompok data tersebut, selanjutnya dilakukan penjumlahan. Hasil penjumlahan kuadrat (sum of squares) tersebut akan selalu bernilai positif.

Nilai varian diperoleh dari pembagian hasil penjumlahan kuadrat (sum of squares) dengan ukuran data (n).

Namun begitu, dalam penerapannya, nilai varian tersebut bias untuk menduga varian populasi. Dengan menggunakan rumus tersebut, nilai varian populasi lebih besar dari varian sampel.
Oleh karena itu, agar tidak bias dalam menduga varian populasi, maka n sebagai pembagi penjumlahan kuadrat (sum of squares) diganti dengan n-1 (derajat bebas) agar nilai varian sampel mendekati varian populasi. Oleh karena itu rumus varian sampel menjadi:

Nilai varian yang dihasilkan merupakan nilai yang berbentuk kuadrat. Misalkan satuan nilai rata-rata adalah gram, maka nilai varian adalah gram kuadrat. Untuk menyeragamkan nilai satuannya maka varian diakarkuadratkan sehingga hasilnya adalah standar deviasi (simpangan baku).

Untuk mempermudah penghitungan, rumus varian dan standar deviasi (simpangan baku) tersebut bisa diturunkan :
Rumus varian (ragam):

Rumus standar deviasi (simpangan baku) :

s2 = varian
s = standar deviasi (simpangan baku)
xi = nilai x ke-i
Contoh:
Misalkan dalam suatu kelas, tinggi badan beberapa orang siswa yang dijadikan sampel adalah sebagai berikut.
172, 167, 180, 170, 169, 160, 175, 165, 173, 170
Dari data tersebut diketahui bahwa jumlah data (n) = 10, dan (n - 1) = 9. Selanjutnya dapat dihitung komponen untuk rumus varian.

Dari tabel tersebut dapat ketahui:



Dengan demikian, jika dimasukkan ke dalam rumus varian, maka hasilnya adalah sebagai berikut.

Dari penghitungan, diperoleh nilai varian sama dengan 30,32.
Dari nilai tersebut bisa langsung diperoleh nilai standar deviasi (simpangan baku) dengan cara mengakarkuadratkan nilai varian.
Dari nilai tersebut bisa langsung diperoleh nilai standar deviasi (simpangan baku) dengan cara mengakarkuadratkan nilai varian.

SIMPANGAN RATA-RATA, RAGAM DAN SIMPANGAN BAKU
![SIMPANGAN RATA-RATA, RAGAM DAN SIMPANGAN BAKU]() Reviewed by TARBIYAH SYAMILAH
on
10:45 PM
Rating:
Reviewed by TARBIYAH SYAMILAH
on
10:45 PM
Rating:


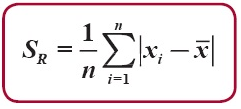
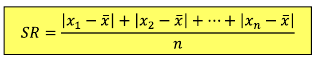
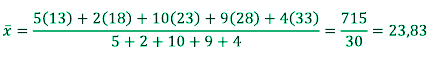
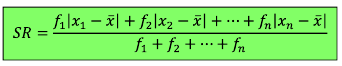
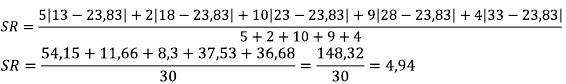
 =
= 



No comments: